PID theory: Time constants
Mastering PID control is largely about mastering the dynamics of the situation, i.e. how things change with time. In our kettle experiment we discovered that the delays in the kettle-water-thermometer system made it difficult to control the temperature.
Most theories of PID control analyse the dynamics in terms of frequency response, with poles and zeros or Bode plots. That's all very well for the mathematicians, but not very helpful if you have neither the math nor the fancy test equipment.
Our approach is different. We will use the time domain response, i.e. how the system changes with time. That is something you can be observe quite easily and understand intuitively.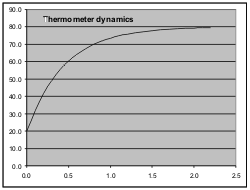
Think back to our electric kettle and the thermometer. Let's take the thermometer out of the kettle and allow it to cool down to room temperature (20°C) and meanwhile heat the water up to 80°C. When everything is stable we stick the thermometer into the water and observe the mercury. Does it go instantly to 80°C? No, it takes time. If you observe carefully you will notice that it moves quickly at first, but as it approaches 80°C it slows down. Mathematically what is happening is that the rate at which the mercury moves (heats up) is proportional to the difference between its instantaneous temperature and the temperature it is heading towards. The closer it gets to the final destination, the slower it moves, because there is less difference to "drive" the change.
The graph shows the readout versus time curve. The following table shows how you can create such a curve for yourself in Excel. The first column is just time, in 0.1 second increments. The second column is the temperature as actually read out. The 3rd column is the difference between the readout and 80°C. The final column is the difference multiplied by 0.2 (or any constant <1).
Now here's the trick: The second readout value is calculated as the sum of the readout in the row above plus the 4th column in the row above. This is repeated right down the table.
| Time (s) | Readout | Difference from 80 | 0.2 * difference |
|---|---|---|---|
| 0.0 | 20.0 | 60.0 | 12.0 |
| 0.1 | 32.0 | 48.0 | 9.6 |
| 0.2 | 41.6 | 38.4 | 7.7 |
| 0.3 | 49.3 | 30.7 | 6.1 |
| 0.4 | 55.4 | 24.6 | 4.9 |
| .... Several rows omitted .... | |||
| 1.3 | 76.7 | 3.3 | 0.7 |
| 1.4 | 77.4 | 2.6 | 0.5 |
| 1.5 | 77.9 | 2.1 | 0.4 |
| 1.6 | 78.3 | 1.7 | 0.3 |
| 1.7 | 78.6 | 1.4 | 0.3 |
| 1.8 | 78.9 | 1.1 | 0.22 |
| 1.9 | 79.1 | 0.9 | 0.17 |
| 2.0 | 79.3 | 0.7 | 0.14 |
| 2.1 | 79.4 | 0.6 | 0.11 |
| 2.2 | 79.6 | 0.4 | 0.09 |
If you have installed PIDassist to the default folder, it will be in C:\Program Files\SPLat\PIDassist. In that folder you will find a subfolder \spreadsheets. In that folder you will find a spreadsheet file named Thermometer.xls. Assuming you have Excel on your computer, you can now examine that file. If you don't have Excel, you can download a free office suite called OpenOffice from www.openoffice.org. This contains a spreadsheet program that will do some of what Excel can do.
What you will see when you launch Thermometer.xls is the original of the above table and graph. Invest a few minutes to explore how each Readout value except the first is calculated from the Readout and Difference in the row above.
Now select Sheet 2 from the tabs at the bottom of the page. What you will see here is a similar page, but with different stuff in the spreadsheet and a second curve added to the graph. In row 4 you will see an entry called "Tau", and if you investigate you will see that Tau is used in the equation for each entry in the Readout column.
Take a look at the equation for the cells in the Readout column. It is of the form:
Reading = 20+60*(1-EXP(-A10/$B$4)) where
20 is the starting temperature
60 is the total temperature change
EXP(...) is the exponential function, meaning the number e raised to the power of something. (e is a number the mathematicians like, something like Pi. Its value is 2.718282....)
A10 is the time value from the lefthand column.
$B$4 is Tau
Let's re-write this into a more "mathematical" form:
Reading(function of t) = Initial_Value + Total_Excursion * (1 - Exp(-t / Tau))
If the Exp (exponential) function seems scary, don't worry. You don't need to understand how it works, but it helps to understand something of how it behaves. It may interest you to know this is the same exponential function that governs compound interest and bacteria growth. But because of the minus sign in front of 't', instead of growing without bound it grows towards a limit it can never quite reach.
OK, back to Sheet 2!
The initial value of Tau is set to 0.6. See if you can find a value of Tau that makes the pink curve exactly overlap the blue curve (which is the one from Sheet 1). Hint: Change Tau by about 0.1 at a time, and observe the effect.
Now look at the other columns in Sheet 2. "°C Change" is simply the Readout column with the 20°C starting value subtracted. "% Change" is the change as a percentage of the total 60°C change. This last column is the most useful one for understanding the curves in a generalised sense, because the numbers are normalised back to percentage change. In that column it won't matter if we are talking °C, rpm, PSI or whatever.
Now go back again to Tau, and set it to 1. Look at the row for t=1 (row 17) and read off the % Change value. It is 63.2%. Alter Tau to 2 and read off the % Change value for t=2 (row 27). It is still 63.2%.
The number Tau is what we call the time constant. When t=Tau, the exponential function becomes Exp(-1)=0.367879 and the term (1-Exp(-1)) becomes 0.632..., which is where the 63.2% number comes from.
Very many systems have a dynamic behaviour that follows the exponential law. If we know the time constant of such a system, we have a good handle on its dynamic behaviour. The time constant can be measured by applying an "input" (voltage, heat, power, pressure) to the system and determining when in time it reaches 62.3% of its final excursion.
As an exercise, fiddle with Tau on the spreadsheet and determine how far the output (% Change) gets in 2 time constants, 3, 4 etc. Also, see if you can find the relationship between Tau and the 0.2 multiplier we used in Sheet 1.
As a matter of interest, Sheet 2 represents the "continuous process" as it takes place in the real world, whereas Sheet 1 represents the sampled system approach that forms the basis of a digital implementation of a PID control loop.
If you are into electronics you will recognize this exponential time constant stuff as being equivalent to a simple Resistor-Capacitor low pass filter with a time constant of R*C.
In the next section we will look at systems that have multiple time constants.
